受験をする上で指標となる偏差値ですが、必要なデータさえあればExcelで算出することができます。
また偏差値とは何かについても少し書いています。
偏差値とは?
たとえば同じ80点を取っても、平均点が90点のテストと60点のテストではその意味合いは変わります。「点数」という絶対数ではなく、平均点に対する自分の得点という形で相対的に自分の成績を数値化したものが偏差値です。
平均点と全く同じ点を取った時は偏差値は50となり、これが基準となります。
標準偏差の求め方
偏差値を求めるには、全体の平均点および標準偏差が必要です。
標準偏差は文字通り「全体の平均にどの程度バラつき(偏り)があるか」を意味し、英語で言うとStandard Deviationとなります。これを略してStdevとなります。
Stdev関数は「全体の中の一部(サンプル・標本)を抽出して全体を推定で計算する場合」に使い、母集団全体のデータが使える場合はStdevP関数を用います。PはPopulation(母集団)の略です。
Stdev関数を使うと、StdevP関数より大きな値が出ます。これは「全体の一部を抽出した場合、全体から取った標準偏差より小さな値が返る」傾向があるからだそうですが、とにかく全てのデータがそろっているのであればStdevP関数、一部のデータから全体を類推するのであればStdev関数を使います。
標準偏差(母集団全体)の計算
StdevP(範囲)
StdevP(範囲)
標準偏差(標本)の計算
Stdev(範囲)
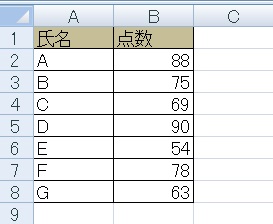
一応Stdev(StdevP)関数を使わないでも、標準偏差を求めることは可能です。実際にやってみると、
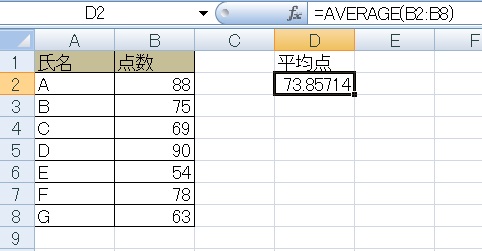
①Average関数で全体の平均をとり、
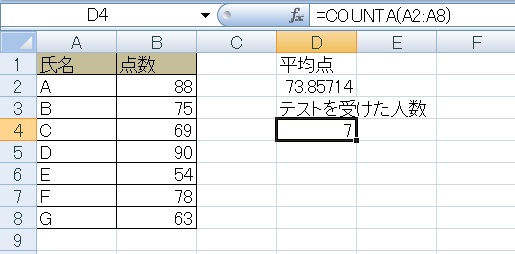
②CountA関数でテストを受けた人数を算出します(この人数なら数字を直接書いてもいいですが)。
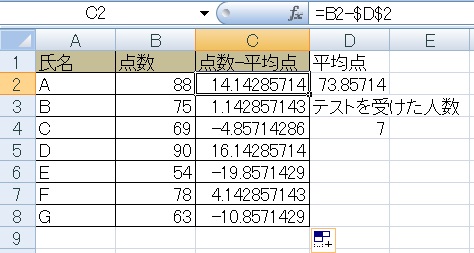
③それぞれの点数から平均点を引き、
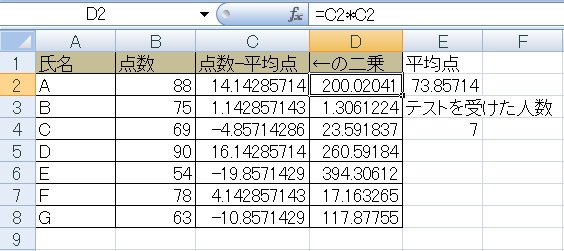
④これを二乗します。この時点で負の数も全て正の数に直ります。
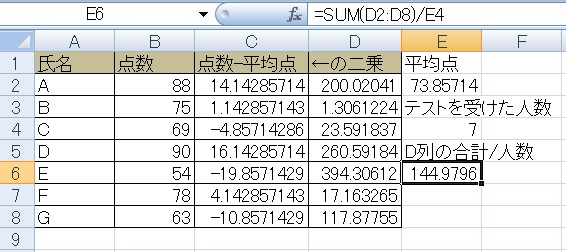
⑤二乗して出た数字を全て合計して人数で割り、
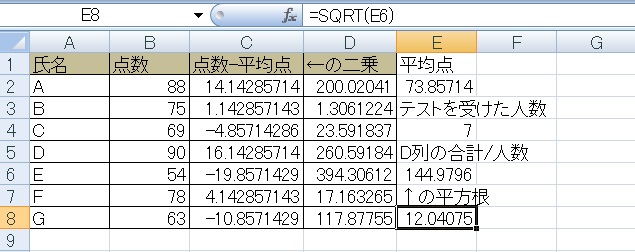
⑥出た数字の平方根をSqrt関数で求めます。これで標準偏差の完成です。
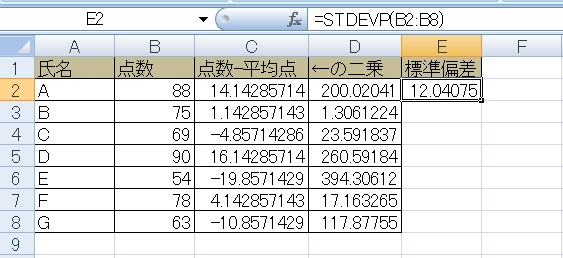
以上の手順をまとめて行うのがStdevP関数です。この場合点数を範囲とし、=StdevP(B2:B8)のように記述します。
StdevとStdevPの違い
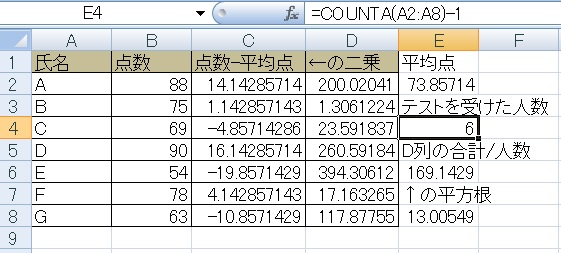
上の手順②で、人数をひとり減らしておくと、少し大きな標準偏差が出ますが、
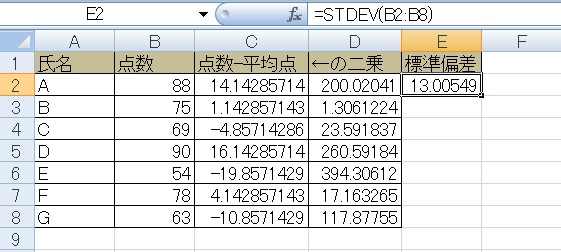
=Stdev(B2:B8)と入力すると、これと同じ値が出ます。StdevPとStdevの違いは、割り算する人数がひとり違うだけです。
Stdev関数とStdevP関数は、計算対象の人数が大きくなればなるほど誤差が小さくなります。
Stdev関数とStdevP関数は、計算対象の人数が大きくなればなるほど誤差が小さくなります。
標準偏差からわかること
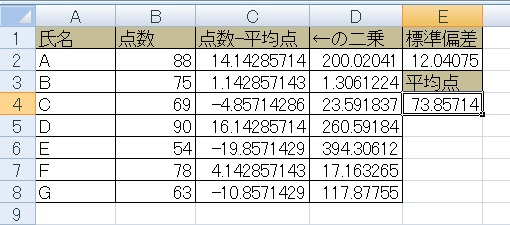
平均点±標準偏差(この場合86~61ぐらい)に、テストを受けたほとんどの人が入る、ということがわかります。
つまり90点取ってる人は飛びぬけて優秀だし、54点取ってる人はかなりマズい、といった見方をすることができます。
つまり90点取ってる人は飛びぬけて優秀だし、54点取ってる人はかなりマズい、といった見方をすることができます。
偏差値の求め方
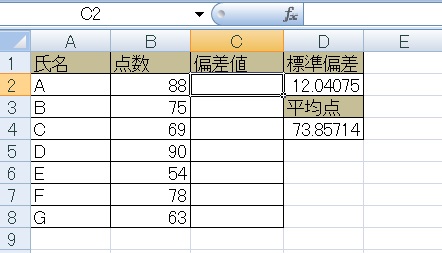
標準偏差を求めたところで、これを使って偏差値も求めたいと思います。偏差値の求め方は以下の通りです。
(得点-平均点)÷標準偏差×10+50
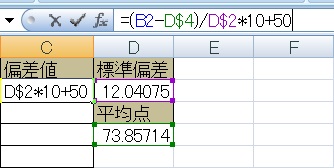
上の式をExcel上で打ちこむと、=(B2-D$4)/D$2*10+50のようになります(D4=平均点、D2=標準偏差)。
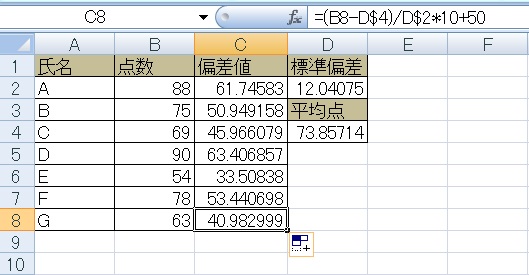
結果このようになりました。
ほぼ平均点の点数をとったBさんの偏差値は50弱となり、平均より約16点高いDさんが63程度に対し、平均より20点近く低いEさんの偏差値は33弱とかなり厳しい数字が出ています。
ほぼ平均点の点数をとったBさんの偏差値は50弱となり、平均より約16点高いDさんが63程度に対し、平均より20点近く低いEさんの偏差値は33弱とかなり厳しい数字が出ています。
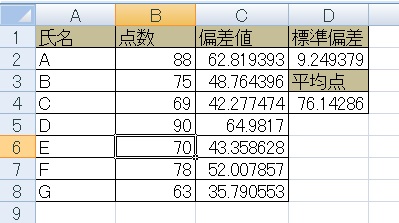
ここでEさんの得点を70点にしてみると、全体の平均が上がり、偏差も少なくなります。すると同じ点数を取った人でもある人は偏差値が上がり、ある人は偏差値が下がり、全体のバランスが再計算されます。
標準偏差および偏差値の求め方については以上です。
やりたいことから方法を探すエクセル(Excel)操作・関数・VBA(マクロ)逆引きまとめ
逆引き(やりたいことから探す)Excel記事まとめ

関数・演算子・メソッド・プロパティ名から探すExcel/VBA(マクロ)使い方・組み合わせ方まとめ
こちらはExcelやメソッドの諸機能を、機能の名称から探せるまとめ記事です。





















コメント